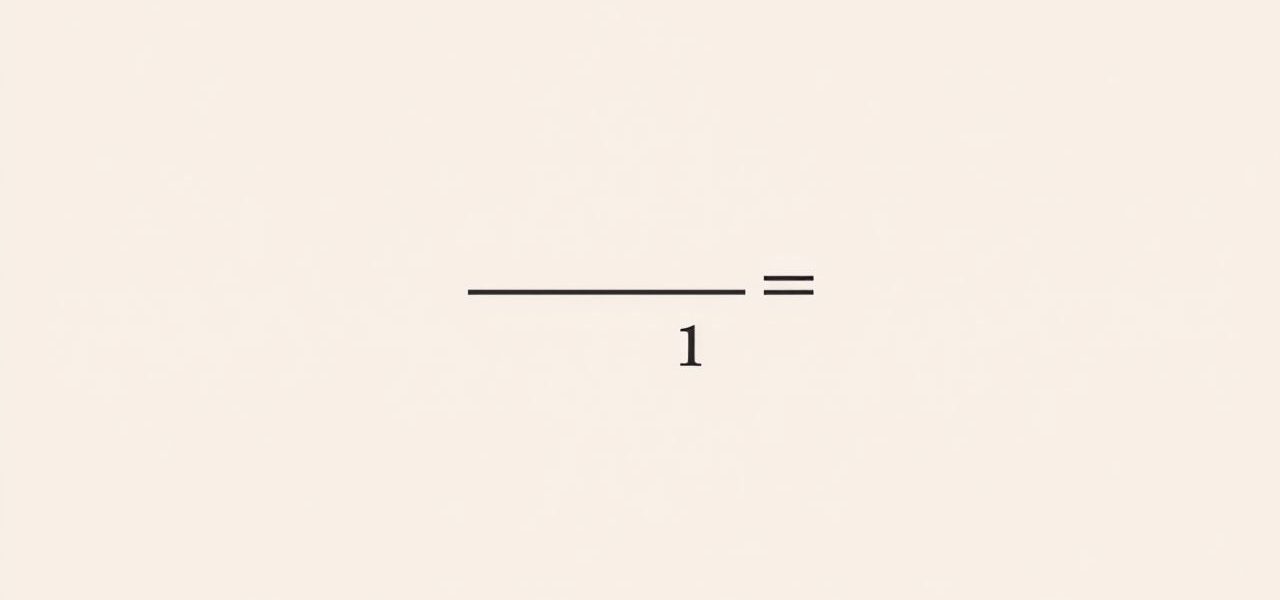When analyzing mathematical functions, one of the most fundamental concepts is that of zeroes, or roots, of the function. The zeroes of a function are the input values for which the function’s output equals zero. Identifying these zeroes is crucial across various areas of mathematics, science, and engineering because they often represent points where behavior changes, solutions to equations, or intersections with the x-axis on a graph. The zeroes provide key insights into the nature of the function and help in solving equations, optimizing processes, and modeling real-world phenomena. This topic explores the concept of zeroes of a function, methods to find them, their significance, and practical examples to understand their role in mathematics.
What Are the Zeroes of a Function?
The zeroes of a function \( f(x) \) are the values of \( x \) for which \( f(x) = 0 \). These are also called roots or solutions of the equation \( f(x) = 0 \). On a graph, the zeroes correspond to the points where the function crosses or touches the x-axis.
Formally, if \( f(x) \) is a function defined on some domain, then any \( x = a \) such that \( f(a) = 0 \) is a zero of the function. Depending on the function, zeroes can be real or complex numbers, single or multiple, distinct or repeated.
Why Are Zeroes Important?
- Solving EquationsFinding the zeroes of functions is equivalent to solving equations, which is fundamental in mathematics and its applications.
- Graph InterpretationZeroes help in sketching graphs by locating intercepts.
- ModelingIn physics and engineering, zeroes can represent equilibrium points, phase changes, or thresholds.
- OptimizationZeroes of derivatives help find maxima and minima of functions.
Types of Zeroes
Zeroes can be categorized based on their nature and multiplicity
1. Real and Complex Zeroes
For polynomial functions, zeroes can be real numbers or complex numbers (involving imaginary units). Real zeroes correspond to visible x-axis intersections, while complex zeroes occur in conjugate pairs and are not seen on the standard Cartesian plane.
2. Simple and Multiple Zeroes
A zero \( x = a \) is simple (or of multiplicity one) if \( f(x) \) crosses the x-axis at \( a \). It is multiple if the function touches the x-axis but does not cross it, corresponding to repeated roots in polynomial equations.
Methods to Find Zeroes of a Function
The method used to find zeroes depends on the type and complexity of the function. Here are some common methods
Analytical Methods
For many algebraic functions, zeroes can be found by solving \( f(x) = 0 \) algebraically
- FactoringExpressing a polynomial as a product of simpler polynomials and setting each factor equal to zero.
- Quadratic FormulaFor quadratic functions \( ax^2 + bx + c = 0 \), zeroes can be found using the formula \[ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \].
- Rational Root TheoremTo test possible rational zeroes of polynomials.
Graphical Method
Plotting the function graphically helps visually locate zeroes by identifying x-intercepts. This is helpful for functions difficult to solve algebraically or for an initial approximation.
Numerical Methods
When algebraic solutions are complicated or impossible, numerical techniques are used
- Bisection MethodRepeatedly narrowing the interval where a zero lies.
- Newton-Raphson MethodUsing derivatives to quickly approximate zeroes.
- Secant MethodAn improvement on Newton-Raphson that does not require derivative calculation.
Properties of Zeroes
Understanding zeroes involves knowing some key properties, especially for polynomials
- Number of ZeroesA polynomial of degree \( n \) has exactly \( n \) zeroes in the complex number system (Fundamental Theorem of Algebra).
- Sum and Product of ZeroesFor quadratic polynomials \( ax^2 + bx + c \), the sum of zeroes is \(-\frac{b}{a}\) and product is \(\frac{c}{a}\).
- Location and BehaviorZeroes can be real and distinct, real and repeated, or complex conjugates.
Examples of Zeroes in Different Functions
Polynomial Functions
Consider the quadratic function \( f(x) = x^2 – 5x + 6 \). To find zeroes, solve \( x^2 – 5x + 6 = 0 \). Factoring gives \((x – 2)(x – 3) = 0\), so zeroes are \( x = 2 \) and \( x = 3 \). These zeroes correspond to points where the graph touches the x-axis.
Trigonometric Functions
For \( f(x) = \sin x \), zeroes occur where the sine function crosses the x-axis. These are at multiples of \( \pi \), or \( x = n\pi \), where \( n \) is any integer.
Exponential and Logarithmic Functions
Functions like \( f(x) = e^x – 1 \) have zeroes where \( e^x = 1 \), which is \( x = 0 \). For logarithmic functions such as \( f(x) = \log x \), zeroes occur where the argument of the log is 1 (since \( \log 1 = 0 \)). Thus, the zero is at \( x = 1 \).
Significance of Zeroes in Calculus
In calculus, zeroes of functions and their derivatives are crucial. The zeroes of a function indicate points where the function crosses the x-axis. Zeroes of the derivative, \( f'(x) = 0 \), are critical points that help identify local maxima, minima, or inflection points. These concepts are essential in curve sketching, optimization problems, and analyzing the behavior of functions.
Real-World Applications of Zeroes
The concept of zeroes extends beyond pure mathematics and has numerous practical applications
- PhysicsZeroes can represent equilibrium points in mechanical systems.
- EngineeringUsed in control systems to analyze system stability.
- EconomicsZeroes of supply-demand functions represent equilibrium prices.
- BiologyZeroes of growth models indicate population thresholds.
The zeroes of a function are fundamental in understanding and analyzing mathematical functions. They serve as critical markers where the function’s output changes sign or behavior, providing solutions to equations and insights into graphs. From algebraic equations to trigonometric and exponential functions, identifying zeroes is a key skill in mathematics, science, and engineering. Various methods, ranging from analytical to numerical, assist in finding zeroes accurately. Grasping the concept of zeroes enhances problem-solving abilities and equips learners and professionals alike to tackle complex problems in diverse fields effectively.